【转载】Tensorflow入门教程（译文）

Tensorflow 提供了很多 API，最底层的叫 TensorFlow Core ，它提供完整的编程控制（我理解就是说底层控制）。我们推荐搞机器学习的研究人员或者其他的想对自己的模型有一个很好的控制的人用 TensorFlow Core 。

本教程从 TensorFlow Core 开始讲。接下去我们会展示怎么用 tf.contrib.learn 来实现等价的模型。在你用其他的一些更高级紧凑的 API 的时候，知道 TensorFlow Core 的原则会使你大脑里面有关 tf 内部是怎么工作的图景更清楚一些。

原作者：npa（开源社区）
作者博客：http://science.npa.farbox.com/
*转载已获作者授权

Before Starting

本教程将带你开始用tensorflow编程。读之前先安装tensorflow。要搞懂这个教程的大部分内容，你至少要：

• 会写python
• 至少懂一点数组
• 最好是会点机器学习，不过不怎么懂或者完全不懂也没事，这仍然是你的第一篇教程。

名词解释：Tensors

TensorFlow中核心的数据单位就是 tensor 。一个 tensor 就是一个装了原始数据任意维度的数组。维度叫做rank。举几个例子：

• [] - 空数组，rank 为 0 的 tensor

• [1., 2., 3.] - rank 为 1 的 tensor，也就是一个 shape 是 [3] 的向量

• [[1., 2., 3.], [4., 5., 6.]] - rank 为 2 的 tensor，也就是一个 shape 是 [2, 3] 的矩阵
• [[[1., 2., 3.]], [[7., 8., 9.]]] - rank 为 3 的 tensor，shape 是 [2, 1, 3]

TensorFlow Core 教程

导入TensorFlow

权威的导入方法是这样的：

import tensorflow as tf

这样就让 Python 可以访问所有 TensorFlow 类、方法和符号。大部分的教程默认你已经做过这步了。

计算图 The Computational Graph

可以把TensorFlow Core编程想成两部分：

1. 构造计算图
2. 运行计算图

计算图 Computational Graph 这个概念就是把一系列的 TensorFlow 操作组织成一个由节点组成的图。

下面来建个简单的计算图试试看：

每个节点输入 0 或多个 tensor，输出一个 tensor 。常量 constant 就是一种节点，它不需要输入，输出的值是存储在自己内部的。我们可以来构造两个浮点数常量 tensor node1 和 node2。

node1 = tf.constant(3.0, tf.float32)
node2 = tf.constant(4.0) # 隐式的tf.float32
print(node1, node2)

输出：

Tensor("Const:0", shape=(), dtype=float32) 
Tensor("Const_1:0", shape=(), dtype=float32)

注意了，print 出来的结果不是 3.0 和 4.0，因为 node1 和 node2 是节点，会产生 3.0 和 4.0 这样的 tensor 的节点。要真正求节点的值就要用 session。session 封装了 TensowFlow 运行的控制和状态。

下面的代码建立一个Session对象然后用它的run方法来跑这计算图，然后求 node1 和 node2 的值。

sess = tf.Session()
print(sess.run([node1, node2]))

应该看到输出：

[3.0, 4.0]

用操作节点来把不同的 Tensor 结合到一起就可以构造更复杂一点的计算。比如说我们可以把两个常量加起来得到新的计算图：

node3 = tf.add(node1, node2)
print("node3: ", node3)
print("sess.run(node3): ",sess.run(node3))

这样就得到输出的结果是

node3:  Tensor("Add_2:0", shape=(), dtype=float32)
sess.run(node3):  7.0

TensorFlow 提供了一个叫 TensorBoard 的功能来可视化计算图。截图如下：

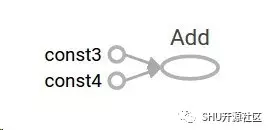
这图什么太大意思，因为它就是输出个常量。不过一个计算图可以用参数来表示获得外部输入，称之为占位符 （placeholder）。占位符就是保证接下来这个位置会被提供一个值。

a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
adder_node = a + b  # +号提供了tf.add(a, b)的快捷方法

这三行代码有点像所谓的函数或者是 lambda 表达式，因为定义了两个输入参数 a 和 b，然后执行了一个操作。我们可以传入 feed_dict 这个参数，明确指定提供具体值的 tensor，来算这个图的值。

print(sess.run(adder_node, feed_dict = {a: 3, b:4.5}))
print(sess.run(adder_node, feed_dict = {a: [1,3], b: [2, 4]}))

输出：

7.5
[ 3.  7.]

TensorBoard中的结构是这样的：

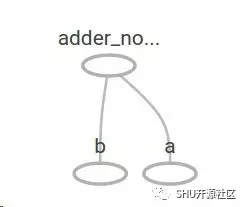
也可以再加一些操作，让计算图变得更加复杂，比如：

add_and_triple = adder_node * 3.
print(sess.run(add_and_triple, {a: 3, b:4.5}))

得到输出

22.5

现在的计算图是这个样子的：

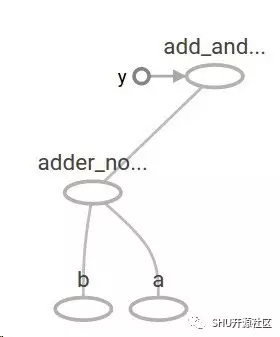
最典型的就是在机器学习里面我们就想要一个模型可以接受这样的任意输入，这一点已经解决了。接下来要让这个模型变得可训练，就要有变量这个概念，让模型（在训练前后）对于相同的输入能给出不同的输出。变量 Variables 允许我们向图里加可以训练的参量。变量由类型和初始值来构造：

W = tf.Variable([.3], tf.float32)b = tf.Variable([-.3], tf.float32)
x = tf.placeholder(tf.float32)
linear_model = W * x + b

用 tf.constant 建立一个常量的话，它马上就被初始化然后值就永远不变了。与之不同的是，变量在执行 tf.Variable 的时候是不被初始化的。要初始化 TensorFlow 项目中的所有变量，还要显式地执行以下操作：

init = tf.global_variables_initializer()
sess.run(init)

理解这点很重要。init 是一个要求 TensorFlow 子图初始化所有变量的操作，在做 sess.run(init) 之前，所有的变量都是未初始化的。

我们可以一齐输入好几个 x 来计算 linear_model 的值：

print(sess.run(linear_model, {x:[1,2,3,4]}))

产生输出：

[ 0.      0.30000001  0.60000002  0.90000004]

现在我们建立了一个模型，但是还不知道这个模型好不好。为了在一些训练数据上面评价这个模型，我们需要一个 y 占位符来提供目标输出，还要写一个损失函数。

损失函数是用来丈量现在这个模型和给定的真实数据之间的差距的。对于线性模型来说，一个标准的损失函数可以是模型给出的值和真正目标输出之间差的平方和。

linear_model - y 就可以得到一系列模型输出值和目标输出值的差，这个结果是一个向量，每一个元素就是一个差。我们用 tf.square 平方一下这个差。然后用 tf.reduce_sum 方法把他们都加起来就得到了总的平方差的量了。

y = tf.placeholder(tf.float32)
squared_deltas = tf.square(linear_model - y)
loss = tf.reduce_sum(squared_deltas)
print(sess.run(loss, {x:[1,2,3,4], y:[0,-1,-2,-3]}))

结果这个损失量是：

23.66

我们可以手工来改变 W 和 b 的值来减小这个差距。tf.assign 可以改变初始化过的变量的值，很明显这里让 W=b=-1 就行了。

fixW = tf.assign(W, [-1.])
fixb = tf.assign(b, [1.])sess.run([fixW, fixb])
print(sess.run(loss, {x:[1,2,3,4], y:[0,-1,-2,-3]}))

这个正好是我们数据的分布，所以损失就是 0 ：

0.0

这里我们猜出了 W 和 b 的完美值，不过机器学习的目的就是自动去找到正确的模型参数。下一节我们展示如何来做到这一点。

tf.train API

对于机器学习比较的完备讨论已经超出了这个教程的探讨内容。不过可以简单地说，TensorFlow 提供了优化器 optimizer，这些优化器可以缓慢地改变各个变量，使得损失函数最小化。最简单的优化器是随机梯度下降（gradient descent）优化器。GD 会对 loss 函数里面的某一变量求导数，然后根据这个导数的值去改变对应的变量。总的来说用参量符号去手动求微分是一个又无聊又容易出错的过程。因而，给定一个模型的描述，用 tf.gradients 方法，TensorFlow 可以自动生成对应导数。简单起见，优化器可以帮你做这件事。举例来说：

optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
sess.run(init) # 把变量的值重置为不正确的随机值
for i in range(1000):
  sess.run(train, {x:[1,2,3,4], y:[0,-1,-2,-3]})
print(sess.run([W, b]))

结果：

[array([-0.9999969], dtype=float32), array([ 0.99999082],
 dtype=float32)]

到这里我们真正意义上实现了机器学习！达成这个简单的线性回归不需要很多 TensorFlow code 的代码，不过如果要构建更加复杂的模型和方法就使得写更多的代码了。因此 TensorFlow 为公共的一些模式、结构和功能提供了更加高层次的抽象。下一节，我们将会学习如何使用这些抽象。

完整代码

tf.contrib.learn 并不会把你限死在预定义的模型里。假如说我们要建立一个定制化的模型，在 TensorFlow 里面又没有预制，我们依旧可以使用 tf.contrib.learn 的一些高级的抽象，包括数据集、feeding、训练，等等。为了说明这个问题，我们将会展示如何利用我们的知识和更底层的 TensorFlow API 来实现我们自己的等价于 LinearRegressor 的模型。

来利用 tf.contrib.learn 定义一个定制的模型，我们需要使用 tf.contrib.learn.Estimator。实际上 tf.contrib.learn.LinearRegressor 就是 tf.contrib.learn.Estimator 的一个子类。这里我们直接传给 Estimator 一个 model_fn 函数，告诉 tf.contrib.learn 如何验证预测结果、训练程度和损失。代码如下：

import numpy as np
import tensorflow as tf
# 声明一系列的特征，我们只需要一个单值特征。
def model(features, labels, mode):
  # 建立一个线性模型来预测值
  W = tf.get_variable("W", [1], dtype=tf.float64)
  b = tf.get_variable("b", [1], dtype=tf.float64)
  y = W*features['x'] + b
  # 损失函数子图
  loss = tf.reduce_sum(tf.square(y - labels))
  # 训练子图  
  global_step = tf.train.get_global_step()
  optimizer = tf.train.GradientDescentOptimizer(0.01)
  train = tf.group(optimizer.minimize(loss),
                   tf.assign_add(global_step, 1))
  # ModelFnOps 方法把我们建立的子图和适当的方法结合起来。
  return tf.contrib.learn.ModelFnOps(
      mode=mode, predictions=y,
      loss=loss,
      train_op=train)
estimator = tf.contrib.learn.Estimator(model_fn=model)
# 定义数据集
x = np.array([1., 2., 3., 4.])
y = np.array([0., -1., -2., -3.])
input_fn = tf.contrib.learn.io.numpy_input_fn({"x": x}, y, 4, num_epochs=1000)
# 训练
estimator.fit(input_fn=input_fn, steps=1000)
# 验证模型
print(estimator.evaluate(input_fn=input_fn, steps=10))

运行后输出结果

{'loss': 5.9819476e-11, 'global_step': 1000}